Расчет устойчивости склона
Расчет устойчивости склона осуществляется различными методами, которые исходят из основного условия равновесия, определяющегося из схемы сил, действующие на склон.
Каковы бы ни были причины, вызывающие нарушение устойчивости склонов, в конечном счете движение горных масс происходит под действием силы тяжести. Следовательно, во многих случаях условия устойчивости склонов могут быть определены по правилам механики.Для расчетов устойчивости разработано много методов.Однако все эти методы исходят из основного условия равновесия , определяющегося из схемы сил, действующих на склон.
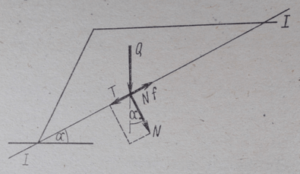
Рассмотрим какой либо склон и проведем секущую плоскость I-I ( рис-1). Примем, что сила тяжести отсеченной части равна Q.Сила тяжести действует вертикально и по отношению к плоскости I-I должна быть разложена на две силы :
касательную Т=Q sin α и нормальную N=Q cos α.
Сила Т вызывает смещение горной массы по плоскости I-I, а сила N создает силу трения Nf, препятствующую такому смещению. Кроме того, смещению препятствуют силы сцепления с, действующие в плоскости I-I по всей площади, равной F.
Если угол α примет значение αкр, соответствующее состоянию предельного равновесия, то можно составить уравнение предельного равновесия: Hf+cF-T=0 или T=Nf+cF; Полученные выражения могут быть преобразованы.Нормальное давление на единицу площади сдвига
σ=N/F=Q cos αкр/F;
Сдвигающее усилие на единицу площади сдвига τ=T/F=Qsin αкр/F. Критическое значение угла α, при котором наступает состояние предельного равновесия, называют углом сдвига ψ.С учетом сказанного уравнения предельного равновесия примут вид:
tgψ =tg φ +c/σ и τ=σ tg φ+c.(1.1)
Из полученных равенств видно, что угол сдвига ψ-величина переменная и зависит от величины нормального давления на поверхность сдвига. Следовательно, поверхность сдвига криволинейна и только при отсутствии в породе сил сцепления обратится в плоскость.Если в равенство (1.1) вместо величины ψ=αкр подставить какое-либо другое значение α, то можно построить ряд поверхностей, проходящих через подошву склона.
Рисунок-1. Схема сил, действующих по плоскости оползания
Очевидно, склоны , образованные поверхностями с углом α>αкр-неустойчивы.Следовательно, угол сдвига ψ=αкр может быть назван предельным или критическим углом устойчивости откоса , а соответствующая ему поверхность склона -предельной или критической поверхностью.
При определении устойчивости того или иного природного или искусственного склона могут встретитьсядве основные задачи: поверхность скольжения заранее известна и требуется только проверить устойчивость склона и поверхность скольжения неизвестна, требуется проверить устойчивость склона и, если это возможно, построить критическую поверхность скольжения.Во многих случаях применительно к одному же склону часто приходится решать обе задачи.
Проверка устойчивости склона с заранее известной поверхностью скольжения
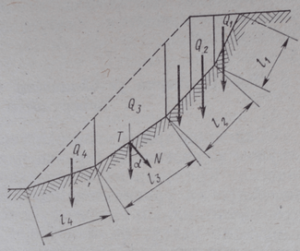
У склонов консеквентного типа с падением слоев напластования согласно склону или покрытых делювиальным плащом поверхность скольжения известна заранее. Для проверки укстойчивости скольжения разбивается на ряд отсеков с размером, перепендикулярным плоскости чертежа, равным единице ( рисунок-2).Тогда сила тяжести каждого отсека на единицу длины будет равна его площади, умноженной на объемную силу тяжести породы и приложена в центре тяжести каждой площади.
Q=1Fϒоб
Продолжим линию действия силы Q до пересечения ее с поверхностью скольжения и разложим на нормальную и тангенциальную составляющие. Тогда очевидно, что N=Q cos α и Т=sin α, где α-угол наклона поверхности скольжения к горизонту в данной точке.Суммируя действие всех сил, получим значение коэффициента устойчивости, как частное от деления всех сил, удерживающих массив от сдвижения на сумму всех сил, вызывающих сдвижение:
η=(∑Nf+∑cl)/∑T=(∑Qcos α tgφ +∑cl/(∑Qsin α), (1)
где с-сила сцепления, т/м ²; l-участок дуги скольжения в пределах данного отсека, м; φ -угол внутреннего трения.При значениях η >1 склон устойчив и подвижки по контактному слою не будет,
при η<1 склон неустойчив и подвижки возможны.Значения η=1 соответствуют состоянию предельного равновесия.Заметим, что в подвижках асеквентного типа после начала движения силы сцепления между сдвигающейся массой и неподвижной частью склона по большей части отсутствуют и выражение (1) примет вид:
Рисунок-2. Схема расчленения скользящего массива на отсеки
η= tgφ ∑Qcos α /∑Qsin α ; (2)
В этом случае поверхность скольжения на плоскости разреза будет изображаться прямой или ломанной. если поверхность склона ломанная, то углы α будут неодинаковы. Сумма сил ∑Т, вызывающих сдвиг, определяет величину оползневого давления. Значение этой величины необходимо для расчета противооползневых мероприятий. В тех случаях, когда поверхность скольжения ломанная, для определения величины оползневого давления следует найти равнодействующую сдвигающих усилий.
Проверка устойчивости склона при неизвестной заранее поверхности скольжения
Основной прием проверки устойчивости был предложен Фелениусом и развит К. Терцаги для откоса, сложенного однородной массой. Криволинейная поверхность сдвига описывается тригонометрическим уравнением второго порядка, близким к уравнению кругового цилиндра, поэтому для упрощения расчетов поверхность сдвига по методу Феллениуса -Терцаги принимают за круглоцилиндрическую.
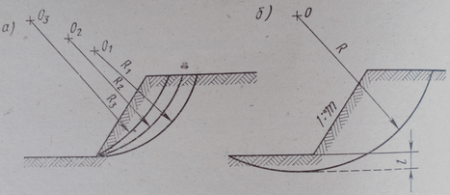
Рисунок-3. Круглоцилиндрические поверхности скольжения проходят через нижнюю кромку откоса (а) или ниже ее(б)
Рассмотрим какой-либо склон ( рис-3), из которого очевидно, что через этот склон можно привести как угодно много круглоцилиндрических поверхностей, каждую из которых можно условно рассматривать как поверхность скольжения. Для каждой из этих поверхностей можно найти радиус R и центр О. Коэффициенты устойчивости, вычисленные для каждой из поверхностей скольжения будут различны. Очевидно, действительная поверхность скольжения совпадает с наиболее опасной условной поверхностью, для которой коэффициент устойчивости наименьший.
Если при этом окажется что наименьший коэффициент устойчивости меньше единицы, то склон будет неустойчив. При наименьшем возможном коэффициенте устойчивости, большем единицы, склон будет устойчив. Основной задачей в этом методе является нахождение самой опасной поверхности скольжения. Решению этой задачи было посвящено много исследований и предложений. При этом возникают две трудности: во первых, надо найти центр наиболее опасной поверхности скольжения и, во вторых, решить, проходит ли поверхность скольжения через подошву склона( рис-3, а) или же ниже подошвы склона ( рис-3, б).
В большинстве случаев принимают, что наиболее опасная поверхность скольжения проходит через подошву склона. Следовательно, решения, соответствующие такой предпосылке, позволяют находить условия устойчивости склонов только для оползней деляпсивного типа. В детрузивных оползнях наиболее опасная поверхность скольжения проходит на некоторой глубине ниже подошвы склона . При расчетах устойчивости эту глубину принимают или исходя из геологического строения склона, или ( условно) как некоторую долю от высоты склона.
Различные приемы определения устойчивости склонов были предложены Н.Н. Масловым, Н.А. Замариным и другими исследователями.Далее приводится основной, наиболее общий метод исследования устойчивости, получивший название полуграфического.
Полуграфический метод исследования устойчивости откоса по Фелениусу-Терцаги
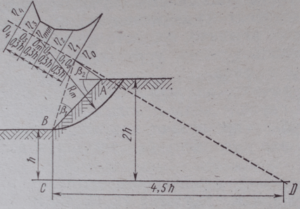
В основу полуграфического метода положено предположение, что круглоцилиндрическая поверхность скольжения проходит через подошву склона .В многочисленных исследованиях различных авторов было установлено, что при заданных условиях центры наиболее опасных поверхностей лежат в более или менее ограниченной зоне. Отложим от подошвы откоса вниз ( рис-4) величину, равную высоте откоса h, и от полученной точки С отложим по горизонтали отрезок CD, равный 4,5h. Проведем линии АОº и ВОº, откладывая их под углами β1 и β2 будем брать в зависимости от уклона откоса ( таблица-2)
Таблица-2. Уклоны откоса в градусах
Через точки D и Оº проведем прямую DОº .Подтверждено вычислениями, что наиболее опасные центры скольжения будут лежать на данной линии. Кроме точки Оº , пометим еще точки О1, О2 и так далее , находящиеся одна на другой на расстоянии примерно около 1/3 высоты откоса h. Приняв точки Оº, О1,О2 и так далее за центры проведем окружности радиусами R0, R1, R2, проходящие через подошву откоса В.Полученные участки откоса разобъем на отсеки и определим величину сдвигающих и удерживающих сил.
Рисунок-4. Нахождение наиболее опасной дуги скольжения по Феллениусу -Терцаги
Отношение моментов этих сил относительно соответствующих центров скольжения дает величины коэффициентов устойчивости η. Контрольное построение заключается в том, что из точек Оº, О1,О2 и так далее на перпендикулярах к прямой DОº откладывают полученные значения η. Проводим через три точки плавную кривую и строим касательную к ней, параллельную линии DОº, дает наименьшее значение η. Если это значение η >1, то откос устойчив.
Недостатком метода является его громоздкость, требуется много построений и вычислений. Кроме того, условные поверхности скольжения обязательно проводятся через подошву склона, что не всегда соответствует истине. Как уже указывалось в склонах детрузивного типа истинная поверхность скольжения проходит ниже подошвы склона, поэтому наряду с основным методом Феллениуса -Терцаги разработано много других упрощающих расчетно-графические операции и позволяющих использовать их при любых очертаниях поверхности скольжения. Изучение этих методов относится к механике грунтов и в данной статье не рассматриваются.
*****

Добавить комментарий